

 |
 |
|
Навигация
|
Главная » Мануалы С точкой соедине1Н1Я кривошипа и uiaTyna и которая перемещается поступательно. Решение. Относительное движегже UEaiyEia АВ является вращением вокруг оси, перпендикулярной к плоскости рисунка и проходящей через точку А. Положение шатуЕЕа в этом движсееии определяется углом 4= l XiAB= 1 АВО. По теореме сиЕЕусов имеелЕ: sin 9 siH 9 = arcsin {- sin uit Это - уравнение отЕЮСительного движения шатуна АВ. ЧтобьЕ ЕЕОлучить уравЕШния относительного движения ползуЕЕа В, достаточЕЕО выразить его отиосительЕ1ые коордиЕЕЗты Xi, yi через най-дешЕый угол (Jj: yi - - I sin ]) - - r sin U) f. Таким образом, в дзенюй задаче сложное движеЕше шатуна АВ разложено еш два ЕЕростых вращательных движсееия: переносное дви-жеЕЕие - вращение с еюстояетной угловой скоростью вокруг ucEirpa О нсЕЕОДвижЕЕЫх осей Оху и относительЕюе движеЕше - неравЕЕОмерЕЕое вращение шатуна вокруг цсЕттра Л Еюдвижной системы координат ху Vj. Задача 5.6. Точка М движется с постоянной скорое еьео вдоль диаметра АВ диска, ЕЕричем в на-чальный момеЕтт точка Етаходилась в центре диска О. Диск одновременно вращается с постоянной угловой скоростью ш вокруг оси, перпендикулярной к рисунку и ЕЕрОХО-дящей через неитр диска. В начальный момент диаметр АВ соввЕЗдал с ОСЬЕО Ох. Определить абсолЕОтиую траек-торшо точки М. Решение. Вращение диска с постоянееой угловой скоростью приЕшмзем за переносЕюе движеЕше. ДвижеЕЕие точеси М по диаметру диска АВ рассматриваем как отЕЕОСителыюе движение. Эту задачу проще всего решить, Ефименив полярную систему коорднЕЕЗт: радиус-вектор ОМ -г, определяющий расстояние точки М от полюса О, и 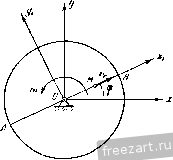 К задаче 5.6. угол (f=£xOxj, определяющий угол поворота радиуса-вектора вокруг точки О. Имеем: Xi = г = Vt, <й = <!)/. Для нахожде1Шя искомой траектории определяем из последнего уравнения время t = и подставляем это значение в первое ypaBiieime г = - . Это есть уравЕ1епие архимедовой спирали в ГЕОлярной системе координат. Задача 5.7. Точка М совершает гармоническое колебательЕ1се движение соглзсеео уравнениям х = 0, з/ = асо8(Дг/ + ?). (1) Экран осциллографа, на котором записывается движение точки Ж, перемещается влево с постояешой скоростью Vg. Определить траекторию, описываемую точкой Л1 на экрзЕЕе (рис. а). Ре ше IE и е. Точка М участвует в сложном движении. Абсолютным или результирующим движением будет Ефямолинейное гармоническое колебательное движеЕЕие точки М по отношеЕШю к Е1еподвижпой системе коорди-Е(зт Оху, определяемое урзвЕЕе-ниями (1). С другой стороны, разложим мысленно абсолютное дви-жеЕше точки М Eia относительное движеЕЕие но отношению к экраЕЕу и переносное движение вместе
к задаче ,5.7. с экраном. Зависимость между коордиЕЕЭтами точки М в абсолютЕЕОм и относительном движениях будет: x = Xq + Xi, У=Уо-\У1, (2) где Xq, у^ - коордиЕЕзты точки Oi, нзчала относительной системы коордиЕЕат, Ху, Уу - искомые коордиЕ13ты точки М в относительном движсЕЕИи. Дзлее, Из (1) и (2) находим: 0 = -V + а cos (А:/+ 8) = О н, далее, xi - vji, у, = а cos {kt р). Исключив из этой системы уравнений время, получим уравнсЕше относительной траектории точки М >i = acos(---i + p . Это уравнение синусоиды. Обозначим длину волны этой синусоиды (рис. б) через /. Тогда время одного полного колебания (период) будет: Таким образом, частота колебаний k точки М связана с длиной волны на экране cooTnouieinieM Для приобретения навыков в peuieiinn задач на определение траекторий и уравнений движения в относительном и абсолютном движениях точки рекомендуется решить следующие задачи из Сборника задач по теоретической механике И. В. Мещерского, изда1[ия 1950 г. и более поздних лет: 417, 418, 419, 422, 423, 425. § 3. Сложение скоростей. Определение скорости точки в относительном, переносном и абсолютном движениях Зависимость между абсолютной, относительной и пере[ЮС[[ой скоростями точки, совершающей сложное (составное) движение, определяется теоремой сложения скоростей, согласно которой абсолютная скорость равна геометрической судше переЕЮСнои и относительЕюй скоростей Va = V,-V,. (1*) Для онределегшя отЕЕОсительной скорости точки следует мыслевшо остановить переносное движение и вычислить относительную скорость по правилам кинематики точки. Для определеЕшя переносЕюй скорости точки достаточно мысленно остановить относительное движение и искать переносную скорость по правилам кинематики точки как скорость той точки перемещающейся 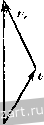 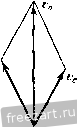 системы координат, с которой совпадает в данный момент движущаяся точка. Теорема сложения скоростей (рис. 5.3) позволяет решать задачи такого рода: 1. Известны две стороны треугольника скоростей по величине п направлению, соответствующие, например, абсолютной и переносной скоростям точки; требуется определить третью сторону треугольника, соответствуюгцую относительной скоростп точки. 2. Известна одна стороЕга треугольника по величине и направлению, соответствующая, например, абсолютной скоростг! точки, а также [Шправленкя двух других CTOpoit. Огфеделить величины пере1[Осной и относительной скоростей. Penjeime этих задач может быть получе[[о графически, построением замк)1утого треуголь[[Ика скоростей (рис. 5.3, а) или параллелограмма скоростей (рис. 5.3, б). При обходе треугольника скоростей стрелки, определяющие направление относительной и переносной скоростей, идут в одном направлении, стрелка, определяющая нагфавление абсо.ютЕЮй скорости, - в противоположном. Рещение задач, таким образом, сводится к построению треугольника или параллелограмма скоростей и определению элементов, сто-ро[[ и углов этих геометрических фигур. Это определение может быть сделано или тригонометрическим путем, или проектирова[[ием геометрического равенства (1*) на декартовы оси иоордшгат. При применении метода проекций надлежит выбрать оси координат и спроектировать равенство (1*) па эти оси. Тогда зависимости между проекциями абсолютной, относительной и переносной скоростей определяются формулами: Величина абсолютной скорости находится по ее проекциям Рис. 5.3. (2*) а ах I ау (3*) Направление абсолютной косинусами скорости определяется направляющими cos( )= cos(v у) = У. (4*) А о) 6) 6} К задаче 5.8. Определить время от выхода з[!ука из А до возвраитепия его в Л„ если скорость распространения звука в воде с. Решение. Первый способ. Разложим абсолютное движе[1не звука со скоростью с на nepeiiocnoe движегЕие вместе с передней лодкой и на относительное движение по отношению к передней лодке. Переносная скорость равна скорости первой лодки так как подвижная система координат связзЕЕа с первой лодкой и движется поступательно. При распрострапепин звука от задней лодки к передней отеюск-тельная скорость звука (рис. а) С этой относительной скоростью звук проходит относительное расстояние s, отделяющее лодки, за [шкоторое время i. Следовательно, (с-У)1 = 5. (1) При решении задач рекомендуется такая последовательность действий: 1) разложить движение па составляющие, опредсл;н1 абсолют[[ое, относительное и переносное движсееия; 2) выбрать две снстсмье координат: абсолютную и подвижную; 3) мысленно оста[[Овив переиосиое движение, найтп скорость относительного движения точки; 4) мысленно отвтекаясь от относительного движения, найти скорость переносного движения точки; 5) [фименив теорему сложен[1я скоростей, определить иском} ю абсолютную скорость течки. Если абсолютная скорость известна, то можно, [юльзуясь теоремой сложения скоростей, найти гско.мую относительную гетп нерепос-пую скорость точки. Задача 6-8. Две подводные лодки плывут друг за другом ш расстоянии s одгЕа от другой с одинаковой скоростью -v. Знук локатора, установленного на задней лодке А, настигает впереди плыву-нгую лодку в точке и, отразиЕикнсь, возвраитается иа экран локатора в точке Ai. в обратном направлении, от передней лодки к задней, звук имеет относительную скорость (рис. б) так как в этом случае абсолютная скорость звука с нанравле1[а вправо, а переносная скорость задней лодки ч) - влево. Звук прохо-дггг относительное расстояние s между лодками зд некоторое время /.>. Следователыю, {c-rv)h = s. (2) Огфеделяя из (1) время /, и из (2) время /.j, складываем их и находим искомое время от выхода звука до его возвращения t = t ~-t - ! - с - V с -\-v с' - V- Второй способ. Обозначим через ti время, в течение которого звук проходит расстояние ABi (рис. в). Тогда расстояние ABt = cti, (3) так как звук проходит этот путь с постоянной скоростью с. С другой стороны, это же расстояние рав[[о начальному расстоянию между лодками АВ плюс расстояние BBj, которое прошла передняя лодка за время ty со скоростью v, т. е. ABi = s-i-vti. (4) Приравнивая (3) и (4), находим: и = -. (5) Обоз[[ачим через время, в течение которого звук проходит рас-стоя[[ие BiAi, отразившись от передней лодки. Это расстояние BiAi = cti, (G) так как звук прошел это расстояние с постоянной скоростью с за время ti- С другой стороны, это расстояние BiA, = ABi - AA, = s-}- vii - (/, -f h), (7) ибо AAi - это путь, пройденный задней лодкой с постоя1Июй скоростью V за время (/] --1). Сопоставляя раве[1ства (6) и (7), получаем, что и -----. Искомое время от выхода звука из А до возвращения его в Ау равно сумме времен ty и U \=A--/., = 2i+-f (8) Подставляя в это уравнение значение ty, определяемое из (5), н решая затем (8) относительно искомой неизвест1[0й t, после несложных преобразований находим, что (.2 -у2 F<aK видно, первый способ, основанный на теореме сложения скоростей, проще и быстрее ведет к нели. Задача 6.9. При запуске искусственного спутшЕка Земли ему необходимо сообщить вблизи поверхности Земли абсолютную горизонтальную скорость 8 км/сек. Определить наименьшую и наибольшую относительные горизонтальные скорости, которые необходимо сообщить сгвутшЕку, если запуск производится на экваторе; на широте 60°; на Северном полюсе. Радиус Земли /? = 6400 км. Решение. Спутник до начала полета вращается вместе с Землей как одно тело. Движение спутника вместе с Землей принимаем за переносное движение. Движение спутника по отношению к Земле рассматриваем как относительное движение. Тогда абсолютная скорость спутника будет: 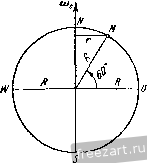 К задаче 5.9. Обозначая широту места запуска углом , получим для определения наибольшей относительной скорости равенство где v = Vr - v, Ve = R cos (f ш^. Запуск спутника в этом случае производится в направлении с востока на запад, в сторону, противоположную вращению Земли. Наименьшая относительная скорость спутника найдется из равенства где Vg также определяется формулой (1). В этом случае запуск производится в направлении с запада на восток, в сторо1\у вращения Земли. При запуске спутника у поверхности Земли на экваторе угол (р = О и, следователыю, = С400 1 /24 . 2г/3600 =: 0,465 км/сек. Наибольшая и наименьшая относительные скорости спутника определятся из равенства или 8 = tv d; 0,465,. откуда максимальная относительная скорость = 8,465 KMJceK, а мп1пшальпая от1ЮСительная скорость = 7,535 КМ/сек. При запуске спутника на широте 60° переносная скорость спут-1Н1ка, равная скорости точки, находящейся у поверхности Земли, будет: Ve, = R cos 60°m, = 0,233 км,сек, и, следовательно, наибольншя и наименьшая относительные скорости спутника определятся из равенства 8 =-л, ±: 0,233, max = 8,233 км/сек, г /-min = 7,767 км/сек. При запуске спутника на Северном или Южном полюсах переносная скорость равна нулю, так как эти точки земной поверхности расположены на оси вращения, и, следовательно, v = v = S км!сек. Задача 5.10. Кривошш! ОА = г вращается в плоскости чертежа BOKjiyr неподвижЕЮй точки О соглас[[0 уравнению v = kt. Ползун А при этом перемещается в накло[[ной кулисе В, которая может [lepe-двнгаться поступательно вдоль осп Ох. Угол наклона кулисы к оси Ох равен а. Составить уравнения абсолют1юго и относительгюго движений точки А, а также найти абсолютную, относительную и перепосную скорости точки. Решение. Первый способ. Абсолютное движение ползуна А - вращение вокруг неподвижного центра О. Относительное движение - прямолинейное движение ползуна вдоль кулисы, определяемое переменным расстоянием OiA = -q. Переносное дпижение - поступательное перемещение точки Л вместе с кулисой. Уравнения абсолютного движения точки А имеют вид x = rcoRkt, y - rsinkt. (1) С другой стороны, обозначая расстояние 00i=x имеем: x = Xg-{-r COS а, у = 4 sin а. (2) Решая совместно уравнения (1) и (2), после неслож[1ых преобразова-1Н1Й находим: Хе = Г COS kt - Г sin kt ctg a. Уравнение (3) является уравнещюм относительного движения точки А. Уравнение (4), с точностью до постоянной величины, является уравнением переносного движения, гак как последнее является поступательным движением. 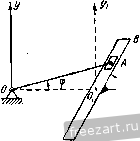 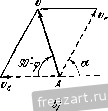 К задаче 5.10. Определим, далее, абсолютную скорость точки А. Так как проекции скорости Vx-x = -гk sin kt, Vy=y = rk cos kt, TO модуль абсолютной скорости v = VT=rk, a направляющие косинусы имеют вид COS (v, х) = - = - Sin kt, cos (v, y) = - = cos kt. (5) Из (5) видно, что абсолютная скорость точки А перпендикулярна к кривошипу ОА. ~ cos (kt - а) Отсюда 1[аходим модуль от[[осигель[[ой скорости , cos kt = rk --. sm ot Проекция переносной скорости на ось х будет: vx - - гЛ (sin kt-\- cos kt ctg я). Второй способ решения быстрее и проще ведет к цели, если требуется определить только скорости в абсолютном, переносном и относительном движениях. Если же необходимо, кроме этих скоростей, найти и уравнения абсолютного, переносного и относительного дви-же1[ий, то целесообразно применить первый способ решения. Задача 6.11. Точка М скользит по наклонной плоскости АВ призмы с относительной скоростью, модуль которой равен проекция относительной скорости точки А на направление ОИ равна производной от относительной координаты по времени , cos kt i sma так как относительное движение является прямолиьгейным. Проекция переносной скорости точки А на ось х vx = Хе = - rk sin kt - rk cos kt ctg Я, так как переносное движение является поступательным и, следовательно, скорости всех точек кулисы одинаковы. Второй способ. Находим величину угловой скорости кривошипа OA (О = <f = А;. Величина абсолютной скорости точки А как конца кривошипа, вра[цаго[цегося вокруг ненодвнжЕЮго цс[1тра О, г> = гш = гА. Иа[1равлена эта скорость перпеь[дпкулярно к кривониту. Относительная скорость точки А направлена вдоль прямой OiA. Переносная скорость точки А параллель[1а оси Ох. Строим параллелограмм скоростей (рис. б). Откладываем вектор, равный абсолютной скорости точки А. На этом отрезке, как на диагонали, строим параллелограмм скоростей, проводя липни, параллельные относительной и переносной скоростям, величины которых неизвестны. Эти величины определяются как стороны параллелограмма. По теореме синусов имеем: 1 ... 28 29 30 31 32 33 34 ... 51 |
 |
 |