

 |
 |
|
Навигация
|
Главная » Мануалы Модули нормальных ускорений точек соприкосновения обоих колес определяются формулами: 2 = r.i< -i. 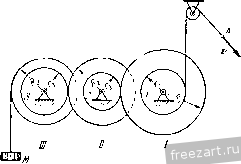 Нормальные ускорения этих точек не равны друг другу по величине и направлены но одной прямой н разные стороны. Задача 4.13. Для спуска груза М, привязанного к копну троса, намотанного на барабан /, вытягивают со скоростью ti канат А, намотанный на барабан 7. На одной оси с барабаном 7 радиуса Г] насажено зубчатое колесо / радиуса /? жестко скрепленное с ним. Зубчатое колесо / сцеплено с зубчатым колесом 2 радиуса г. которое вращается как одно целое вместе с зубчатым колесом радиуса R. Последнее сцеплено с зубчатым колесом 3 радиуса Гд, вращающимся как одно целое с барабаном / радиуса Ry Определить скорость, с которой спускается груз М, если оси всех зубчатых колес неподвижны. Р е ш е н и е. Модуль скорости точки на ободе барабана 7 радиуса г, равен величине скорости точек каната V. Определим скорость точки на ободе зубчатого колеса / радиуса Rx. Модуль угловой скорости барабана 1 и зубчатого колеса / равен ш, = -. Величина скорости точки на обеде зубчагого колеса / г), =(i),Rj = Rx. Зубчатое колесо ,/ находится в сцепле1ти с зубчатым колесом 2 радиуса г^, следовательно, скорости точек па ободе этих колес равны. Определяем модуль угловой скорости зубчатых колес 2 и И, далее, находим величину скорости точки на ободе зубчатого колеса радиуса Ri Vi = Ri = R.. 10 м. и. Бать и др., X. i К задаче 4.1,1, Эю И есть одновременно модуль скорости точки на ободе зубчатого колеса 3 радиуса Гд, сцепленного с зубчатым колесом . Следовательно, величина угловой скорости зубчатого колеса 3 и барабана / равна Модуль скорости точки на ободе барабана / радиуса R, равный искомой величине скорости груза М, дается формулой  к задачам 4.14, 4.15. Задача 4.14. Для преобразования периодического возвратно-по-сгунательного прямолинейного движения во вращательное движение в двигателях внутреннего сгорания применяют плоский шатунно-кривошипиый механизм, состоящий из кривошипа ОЛ=л вращающегося вокруг неподвижной точки О в плоскости рисунка, шатуна АЕ = 1, шарнирно соединенного с кривошипом, и поршня В, двигающегося но горизон-1алы1ым направляющим цилиндра, совпадающим с прямой ОВ, и шарнирно соединенного с шатуном АВ. Полагая угловую скорость кривошипа OA постоянной и равной определить уравнение движения и скорость поршня В. Найти скорость поршня при <р, = 0, <sji = r.ll, (рз = 1:. Решение. Угол гюворота кривошипа, вращающегося с постоянной угловой скоростью u) , равен Опуская перпендикуляр из точки А на линию ОВ, находим уравнение движения поршня В х = 0D -f DB = ОЛ cos 9 + Vf - AD = r cos + V/ - r sin Для определения проекции скорости поршня В на ось х необходимо вычислить производную от координаты поршня X по времени: Вх = - = rf7 = - о 5Ш Ш,/ J I г cos Wo< Sin (1) Значение проекции скорости поршня при различных значениях угла поворота кривошипа получаем, подставляя в (1) соответствующие величины: при с?1 = О и рз = я г)д = О, при <р2 - т/2 X = - - -гш, т. е. при (p.j = 7r/2 скорость точки В равна но величине скорости точки Л; направления скоростей этих точек также совпадают. Задача 4.15. В условиях предыдущей задачи определить ускорение поршня В как функцию времени, а также величину этого ускорения в моменты, когда 9, = О, < = г.12, cpir. Решение. Поршень В движется прямолинейно, следовательно, проекция его ускорения равна первой производной от проекции скорости по времени sin ог-р г sin 2м^ = - гч>1 cos 4>at - 2 Y I-rHirf V 2 cos 2<о/ г- sin- 2мл - sin (0/ 2 ( P - r- sin= Тогда значения ускорегшя поршня при различных значениях угла поворота кривошипа будут: при <р1 = 0 при ср.2 = т/2 при <рз = т: о 1 J-* Задача 4.16. Для подъема груза Р служит электрическая лебедка, состоящая из ведущего вала с насаженной на нем шестере1П<ой с числом зубцов 2]. Груз П0Д1Ш- мается при вращении ведомого вала с шестеренкой. Число зубцов шестеренки г^. При этом канат, на котором подвешен груз Р, наматывается на барабан радиусом R. Уравнение вращения ведущего вала имеет вид 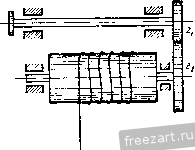 к задаче 4.16. Определить уравнение движения, скорость и ускорение груза Р. Решение. Пути, проходимые точками, расположенными на ободах сцепленных зубчатых колес, равны, т. е. cp, = 9,i = 9if = 2.?i-. Го г, г.. ибо радиусы колес пропорциональны длинам окружностей и, следовательно, пропорциональны числам зубцов. Далее, находим зависимость пути, пройденного грузом, от времени (уравнение движения груза) Проекция скоростп груза па вертикаль определится как производная от координаты но времени Vi=-Si = 4T.Rt Проекция ускорения груза, движущегося прямолинейно, на направление движения равна производной от проекции скорости но времени w.i = Vi = 47:R. Второй способ решения. Определяем проекцию угловой скорости ведущего вала на ось вращения как производную от угла поворота по времени Далее, находим величину угловой скорости ведомого вала, исходя из равенства скоростей точек соприкосновения обоих колес h. (03 г, >. = >, J-=4zfJ-. Скорость груза равна по величине скорости точки на поверхности барабана Vi=Riai = AT.Rtj-. (2) Ускорение груза, движущегося прямолинейно, равно по величине касательному ускорению точки иа поверхности барабана OT, = /?3 = /e=/.4Jl-. Здесь через Г], г, обозначены радиу'сы I п II зубчатых колес, - угол поворота ведомого вала. Из (1) находим: Для определения уравнения движения груза напишем уравнение (2) в виде Vi = = 4.Rt. Умножая обе части равенства на dt, имеем: dSi = 4kR j-1 dt. Интегрируя в пределах от О до s.j и от О до t, находим уравнение движе1шя груза Ж s, = 27:RJW При втором способе решения определяются величина угловой скорости ведомого вала и значение его углового ускорения. Эти величины характеризуют движение ведомого вала и, как частный случай, движение груза А Поэтому второй способ решения предпочтителен. Задача 4.17. Редуктор скорости, предна-значешн^й для измене1шя величины угловой скорости при передаче вращения от вала / к валу , состоит из четырех зубчатых колес, вращаю-нгихся вокруг неподвижных осей. Зубчатые колеса имеют следуюигее число зубцов: 2i=12, 22 = 72, 2з=10. Вал делает 100 об\мин, а вал / должен делать 5400 об/.иин. Найти число зубцов четвертого зубчатого колеса. Грешен и е. Величины угловых скоростей первой нары зубчатых колес, сцепленных друг с другом, относятся обрат!10 нроиорционалыю числам зубцов: Ш, zo Шо z, * К задаче 4.17. Аналогичное равенство можно написать и для второй пары колес, находящихся в зацеплении: 3 4 Колеса 2 и 3 жестко закреплены на общем валу, следовательно, их угловые скорости равны - Перемножая равенства (1) и (2), находим: Отпсшеиие модулей угловых скоростей равно отношению чисел оборе job в минуту. Подставляя известные данные в (3), получаем: £.400 100 12- 10 огсюда следует, что четвертая шестерня имеет 90 зубцов. Задача 4.18. Ведущий вал фрикционной передачи / вращается с носюянпсй угловой скоростью, делая 300 об/мин, и одновременно передвигается в направлении стрелки н обратно согласно уравнению rf=. (4 + 3 cos 20 см, где время дано в секундах. Радиусы колес: г = 5 см, R = 20 см. Определить: 1) угловое ускорение вала как функцию времени и 2) ускорение точки на ободе колеса в моменты времени ti = 0; = 0,25 сек; { - 0,5 сек. К задаче 4.18. Решение. Скорости точек сопри- косновения обоих колес равны между собой, так как колесо / фрикционной передачи катится без скольжения по колесу . Так как величина угловой скорости ведущего вала 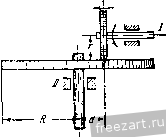 -0 = 300 = 1 Он сек то модуль скорости точки обода колеса /, соприкасающейся с колесом , = == 5 1 Ол = бОгс -cMJceK. (2) Величина скорости такой же точки, но принадлежащей колесу , равна V - 4>d, (3) где cd - модуль угловой скорости колеса . Приравнивая значения (2) и (3), находим величину угловой скорости колеса U 50 л 50л 4 + 3 cos 2r.t сек Проекция углового ускорения колеса равна производной от проекции угловой скорости по времени (считаем, что ось z направлена в сторону <а) doi ЗООл sin 2л^ dt d ЗООл sin 2я (4 + 3 cos 27it) -г сек Переходим к определению ускорения точки па ободе второго колеса в различные моменты времени. Сначала находим для каждого момента времени величины: ш, е. Пользуясь формулами (1), (4), (о), имеем: при ,=0 50,г 507. при .2 = 0,25 CCIC iOj=:- сек г = --сек при 3 = 0,5 сек Мз = сек , £3 = 0. Далее, определяем величину ускорения точки на ободе колеса 11 по формуле Подставляя значения R, £, со для каждого момента времени, находим: Wi = TzlOООО см/сек' = 100м/сек', при <j = 0 при ti = 0,25 сек = Ът -1/75 + 625 с м/сек - = 308 м/сек^, при 3 = 0,5 сек и)з = 50 0007г' 495 000 слДек^ = 4950 м!сек\ Задача 4.19. При пуске в ход кулачок начинает врашагься из состояния покоя вокруг неподвижной оси О с постоянным угловым ускорением £ = 0,1 г сек' -. Достигнув угловой скорости, соответствующей 40 об/мин, кулачок далее вращается равномерно. Уравнение контура кулачка имеет вид г = (,+ 20)с. (архимедова спираль). Стержень А кулачкового механизма движется в неподвижных направляющих В, как показано на рисунке, удерживаясь в соприкосновении с контуром кулачка при помощи пружины. Определить скорость стержня и время, в течение которого продолжался пуск в ход. Найти ус!соре!ше стержня. Решение. Угол поворота кулачка при пуске равен 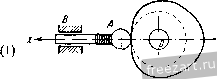 К задаче 4 19. <p = -Jr = 0,05it<*. Расстояние между центром кулачка и стержнем равно -0,05irf2-b20K- - Стержень движется прямолинейно, следователыю, проекция его скорости на ось х равна производной от координаты г но времени Ух = г=--2-\,Ы = Ш см/сек. (4) Проекция ускорения стержня, движущегося прямолинейно, равна производной от проекции скорости по времени Отд; = гг = 3 см/сек . (5) По условию, достигнув угловой скорости, соответствующем 40 об/мин, кулачок далее вращается ргвпомсрно. Модуль угловой скорости последующего равномерного вращения кулачка < i = 40g = lt: (б) Дифференцируя по времени (1), находим проекцию скорости движения стержня па ось х . 30 . 30 30 4 , t , = / = -¥= --(Ui = --1T = 40 см/сек. (7) Пуск в ход продолжается до тех нор, пока скорость (4) не станет равной Vxi- Приравнивая эти два значения скорости, определяем время пуска в ход Т ЗГ=40 или 7=13,33 сек. (8) Время пуска в ход можно определить и другим способом. Проекция угловой скорости кулачка при пуске в ход определяется как производная от угла поворота (2) по времени , = 6 = 0,1::/. (9) Для определения времени пуска Т приравняем значение проекции У1Л0В0Й скорости (9) ее значению (б). Тогда 0,17г7 =4 или 7=13,33 сек. о Задача 4.20. Круговой гоступателыю движущийся кулачок передвигается согласно уравнению (рис. а) х = а cos ш/, где координата х отсчитывается по горизонтали от точки Oj (рпс. б), а, <в - постоянные коэффициенты, / - время. Определить уравнение движения и скорость стержня. Решение. Вводя угол <р, как указано на рис. б, находим координату нижней точки стержня (рис. б) j = rsincp. (1) с другой стороны, расстояние от центра кулачка до начала координат Oi равно jc = r cos<p = acos iot, откуда cos f =-у COS tot, и, следовательно, sin fl 1 - cos ср = 1 - i-J cos t. В  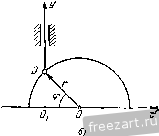 К задаче 4.20. Подставляя это значение в уравнение (1), находим искомое уравнение движения стержня: y = r/l-(ycQSa, . Проекция скорости стержня определится как производная от координаты у но времени а-а sin 2at Vy=S>= -- 2rl/ l-iy] cos Задача 4.21. При подъеме груза А лебедкой закон двнжс1шя груза определяется формулой У = 2-( - cos 9), где h - полная высота подъема, угол ср изменяется пропорционально времени При подъеме груза канат наматывается на барабан В, вращающийся вокруг неподвижной оси О. Определить скорость и ускорение точки на ободе барабана (радиуса R), смысл постоянной До, полное время подъема груза, а также моменты времени, когда угловая скорость и угловое ускорение барабана достигают наибольших и наименьших значений. Решение. Величина скорости точки на ободе барабана равна модулю скорости подъема груза. Проекция скорости груза равна производной от координаты у по времени у=У^-2 sin П или, с учетом (2), Vy = y= у sin 9. Проекция угловой скорости барабана равна 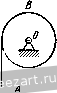 к задаче 4.21. Переходим к определению углового ускорения барабана. Имеем: ег== г = cos ср. Модуль угловой скорости, как это следует из формулы (4), достигает наибольшей величины, когда и, следователыю. sin ср,=± 1, -pi=T-r z, где н = 0, 1, 2, 3, 4, ... Подставляя в (4) значение 9 из (2), находим моменты времени, соответствующие наибольшим значениям модуля угловой скорости. Эги же моменты времени соответствуют обращению углового jCko-рения барабана в нуль, т. е. наименьшим значениям модуля углового ускорения. Наименьшее значение модуль угловой скорости получает при , и, следовательно, при sin 92 = 0 9j = nr.. где n = 0, 1, 2, 3, 4, ... Подставляя в (5) значение угла (2), находим моменты времени, соответствующие наименьшим значениям модуля 1 ... 26 27 28 29 30 31 32 ... 51 |
 |
 |