

 |
 |
|
Навигация
|
Главная » Мануалы находим точку А, в которой этот перпендикуляр пересекается с нормалью к траектории точки. Тогда \QA\ = I Sin <f I Сопоставляя равенства (3) и (4), находим: p = QCl = 2Q, где точка С-центр кривизтл. Задача 3.29. Точка М движется согласно уравнению а = ае , причем уюл, образуемый полным ускорением с касательной, остается неизменным и равным 60°. Определить скорость, касательное, !юрмальное и !Юлное ускорения точки, а также радиус кривизны траектории как функции дуги а. Решение. Проекцию скорости на касательную находим как производную от дуги по времени t, = 3 = ake = k. Проекция ускорения точки на касательную равна Так как угол между полным уско- к задаче 3.29. рением и касательной известен но условию, то модуль 1ЮЛН010 ускорения определится из равепс1ва  W cos а = w, cos 60 Величина нормального ускорения точки будет: Радиус кривизны траектории определяется но формуле ©2 fcV [l3 }/3 k, Радиус гсривизпы с течением времени пеограничепно возрастает. Траектория точки - расходящаяся спираль. 260 дрижЕпиЕ точки !гл. m Задача 3.30. Движение точки задано уравнениями в декартовых координатах X = е' cos t, у = с' sin t, z = e. Определить радиус кривгзш,! траектории. Решение. Для нахождения радиуса кривизны траектории воспользуемся формулой норма/ьного ускорения - = f (О Вычислим скорость точки. Проекции скорости на неподвижные декартовы оси равны Vx = X = е' (cos t - sin t), Vy =y = e (cos t -L sin i\ V, = i = e. Тогда Переходим к определе1пио проекций ускорения точки: Wx=x = - 2е' sin t, Wy = y = 2e cos t, Абсолютная величина ускорешш будет w= [/ w]. -\-W -p w- = e yo. Касательное ускорение находим как производную от скорости по времени: Зиая пеличиш.! полного и касательного ускорений точки, находим ее нормальное ускорение w% = от - от: = 5е2 - Зе = 2е' и, следовательно, и) = е']/2. (2) Внося значения скорости и нормального ускорения в формулу (1), находим радиус кривизны траектории Радиус кривизны и нормальное ускорение являются важными характеристиками движения точки. В да1нюй задаче из уравнения (3) следует, что при неограниченном возрастании времени радиус кривизны неограниченно возрастает. Однако нормальное ускорение не стремится к нулю при неограниченном возрасташш времени, как это видно из (2), а, наоборот, неограничен1Ю возрастает. Траектория точки, заданная параметрическими уравнениями движения, представляет логарифмическую спираль, радиус кривизны которой неограниченно возрастает с течением времени. Задача 3.31. Система состоит из двух блоков (рис. а), один из которых может вращаться вокру1- неподвижной оси О, второй может 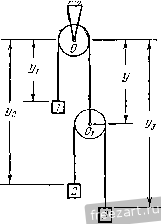 к задаче 3.31. враигаться вокруг подвижной оси Oj. Через первый блок перекинут трос, [1рикрепле1Н1ый одним концом к подвижной оси О,. Груз /, нрикрепленный ко второму концу троса, движется в данный момент вверх со скоростью 6 м/сек и с замедлением 2 м/сек'. Груз 3, нрикрепленный к тросу, перекинутому через подвижный блок, движется вверх с замедлением 4 м/сек', имея в данный момент скорость 3 м/сек. Найти скорость и ускорение центра подвижного блока, точки О, и груза 2 в данный момент времени. Решение. Обозначим ординаты грузов соответственно через yi, yt >з и ординату точки О, буквой у (рис. б). Так как длина троса между грузом / и центром блока Oj неизменна, то У\ + J+ = const, где буквой г обозначен радиус блока. Точно так же неизме1ша и длина троса, соединяющего грузы 2 и 5. Выражаем длину этого троса Уг -У - Ja -У + -г = const. Дифференцируя оба равенства по времеин, находим: )>И-Л-2> = 0. / Подставляя заданные значения скоростей j), н jJj, имеем: р= - 6 м/сек, 1>2 = 2 - j>3= - 15 м/сек. Дифференцируя уравнения (I) но времени, получим: ).+> 3-2j5 = 0. Внося в эти уравне1П1Я известные значения ускорений j?, и у-, находим: у = 2 м/сек ; j?5[ = 2j/-33 = 8 м/сек^. Таким образом, скорость j) и ускорение у точки Oj равны скорости и ускорению груза /, но направлены в противоположную сторону. Скорость J).2 груза 2 направлена вниз и равна 15 м/сек, ускорение этого груза J/.3 направлено вверх и равно 8 м/сек^. Задача 3.32. Ускорение точки равно 12 t м/сек' и направлено по оси х в отрицательном направлении. При = 2 сек скорость точки равнялась 6 м/сек и была направлена по оси х в положительном направле1ши. При t = i сек точка находилась на оси х на расстоя-1НШ 50 м от своего началыюго положения. Определить уравнение движения точки. Решение. Точка движется прямолинейно по оси х, следовательно, ее ускорение в проекции на ось х равно Представим это уравнение в виде dx = ~\1t-dt, (I) умножив обе его части на dt и заметив, что d\x d.i df ~ dt Уравнение (1) интегрируем: Х' = -6/+С,. (2) Для определе1И1я произвольной постоянной интегрирования Ci воспользуемся условием, что при t = 2 сек х = 6 м/сек. Внося эти значения неременных в уравнение (2), находим: G = - 6 2 -}- Q или Ci = 30. Тогда уравнение (2) примет вид х= g = GH 30. Умножая обе части этого уравнения на dt, находим: dx= - 6i4t-20dt Интегрируя, получаем: л- = - 2/ -Ь 30 -\- Q. (3) Чтобы определить гфоизвольную постоянную интегрирования Cj, внесем в уравнение (3) соответственно условию л- = 50 л1 при t3 сек: 50 = - 2 27 + 30 3 + Сз, С,= 14. Внося это значение в уравнение (3), находим уравнение движения точки jc = -2 + 30 + 14. Задача 3.33. В течение 20 сек скорость корабля, совершающего движе1Н1е (циркуляцию) по дуге окружности радиуса 200 м, падает с 15 до 12 м/сек. Предполагая, что величина касательного ускорения пропорциональна квадрату скорости, определить путь, пройденный за первые десять секунд, и угол циркуляции. Р е m е и и е. Касательное ускорение корабля пропорционально квадрату скорости, следовательно. где k - неизвестный но величине коэффициент пропорциональности. Отделяя перемеЕшыс, находим: -- = kdt. 11- Воспользуемся для нахожде1Н1я коэффициента k условием, что в течение 20 сек скорость корабля падает с 15 до 12 м/сек. Интегрируя в этих пределах ураэпсиис (1), имеем: 12 20 ИЛИ = 20/, 1т и k = - 1/1200. Переходим, далее, к определению пути, пройденного кораблем за первые десять секунд. Для этого вначале находим интегрированием из (1) скорость как функцию времени. Имеем: L.c = kt. и Для определения произвольной постоянной интегрирования надо воспользоваться начальными условиями дви'жения: при = 0 скорость v = Vti. Внося эти значения переменных в (2), находим: Подставляя это значение в (2), определяем величину скорости 1 - - v kt Для нахождения длины пути, пройденного кораблем за первые десять секунд, воспользуемся зависимостью Следовательно, 1 ~v H - kvj) Подставляя значения всех вел1Н1ин, получим: 5= 1200 In (1 + 1/1200- 15- 10) = 1200 In 9/8 = 150 м. Тогда угол циркуляции в радианах будет равен 9=:s/R= 150/200 = 0,75. Задача 3.34. Точка движется нрямолийейно с ускорением W - B у^х м/сек', где X - координата точки. В момент времени г', = 2 сек координата точки была Ji:i = 27 м, а скорость равнялась т , = 27 м/сек. Определить уравнение движения точки, а также зависимость ске-рости и ускорения от времени. Решение. Чтобы найти уравнеште движения точки, представим заданную зависимость ускорения от пути в виде и умножим обе части уравнения иа dx, чтобы отделить переменные Интегрируя, находим: dx dv яг - , -bi/xdx, vdv - Gxdx. = -.V3 i c., (1) где Ci - произвольная постоянная интегрирования. Для ее определения подставим в уравнение (1) значения г\ = 27 м/сек при ji:i = 27 Тогда из уравнения (1) получаем С, = 0 и, следовательно, V = ЗхЩ (2) Отделяя переменные и интегрируя, находим: г.пижеппе ТОЧКИ (ГЛ. ГП Используя зависимость v==dx/dt и умножая урапнение (2) иа dt, отделяем переменные Mt. Интегрируя, находим: 3jc 3 = 3M-C,. Произвольную постоянную интегрирования определяем, используя условие задачи: при ti = 2 сек х, = 27 м. Подставляя эти значения в уравнение (3), находим Сд = 3. Уравнение движения точки получим, подставив значение произвольной постоянной в (3): Зависимость скорости от времени найдем, вычисляя производную по времС1Н1 от х: t) = 3( + 1)1 Ускорение как функция времени определится как нроизвод- ная от скорости по времеш!: от = 6 (!f + 1 ). Задача 3.35. Зависимость пройденного пути от времени определяется трапецией, представленной на графике. Начертить график, представляющий зависимость величины скорости от времени (s2 = кореше ние. В течение г.ремени от О до точка движется равномерно со скоростью, равной по модулю Начиная с момента i , до t.i точка Е1еподвижна, ее расстоя.чие от начала отсчета пути остается неизменным. Далее, от момогта t до м( мента 3 точка движется равномерно в обратном направлении со скоростью, равной по модулю Искомая зависимость скорости от времени представлена на рис. б. Задача 3.36. Зависимость величины скорости первой точки от времени изображается дугой полуокружности АМВ. Начальное и К задаче 3.35. конечное значения величины скорости равны т/о- Время движения tj. Определить постоянную скорость с, которую надо сообщить второй точке, чтобы она прошла тот же путь в то же время. Решение. Первая точка прон1ла за время ty путь, равный площади, заключенной между но- . луокружиостью АМВ и отрезком 0D, так как -dl-и, следовательно, s= vdt, о а этот определенный интеграл задаче 3.36. и равен указанной площади. Вычислим искомую площадь как площадь прямоугольника OABD без площади полукруга: , R ti S - Vaty-- - Vftj--2 2 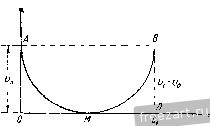 так как численные значения г о и ti/2 равны радиусу окружности. С другой стороны, этот же путь вторая точка должна пройти за то же время, следовательно, s = ct,. (2) Приравнивая оба значения пути (1) и (2), находи.м; откуда величина скорости второй точки равна К задаче 3.37. 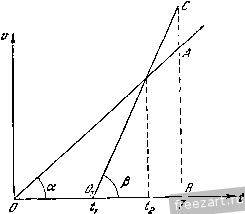 Задача 3.37. Две точки движутся по одной прямой из одного и того же начального положения. Зависимость скорости каждой точки от времени представлена на графике. Известны моменты времени и (см. рисунок). Определить время Т от начала движения первой точки, по ncie-чении которого обе точки встретятся. Решение. Площадь треугольника ОАВ, численно равная пути, пройденному первой точкой за время t, дается выражением ]OB-AB = ]t-i.tga., 1ле через а обозначен угол наклона прямой OA к оси абсцисс. Пло-пидь треугольника OiCB, численно равная пути, пройденному второй точкой за это же время t, выражается так: \OiB-CB = -{t~t{)(t-ti)ig % где через р обозначен угол наклона прямой OjC к оси абсцисс. Точки встретятся в момент Т, когда их нуги будут равны. Следовательно, приравнивая и.ющади треугольников, равные численно пройденным путям, получае.м: 7nga = - (7--f,)Mgp. С Д1)угой сюроны, из траф.1ка следует равенство Решаем совместно систему уравнений (1) и (2). Из уравнения (2) имеем: Подс1авляя это значение в ураипенпе (1) и сокращая обе части равенства на tgi, после несложных преобразований находим: Задача 3.38. Па рис. а представлены зависимости величины ско-pociH от времени для двух прямолинейно движущихся точек, вышед- ших одновременно из одного и того же места. Зависи- мость модуля скорости от времени изображается на графике для первой точки прямой, проходяи1ей через }1ачало координат, для второй точки - четвертью ск-руж1юсти. Определить: 1) ycicopc-ние второй точки как функцию времени; 2) ускорение первой ючки, если известно, что первая точка догоняет вторую точку в юг момент, когда последняя останавливается; 3) вычислить время от 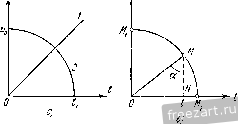 К задаче 3.38. 1 ... 23 24 25 26 27 28 29 ... 51 |
 |
 |