

 |
 |
|
Навигация
|
Главная » Мануалы Первый способ реше1П1я является более удобным, так как определяет скорость и ускорение точки через угловую скорость и угловое ускорение, общие для всех точек тела. Задача 4.5. При пуске в ход мащипы для кручения капроновой нити шпиндель веретена приобретает рабочую скорость, соответствующую 15 000 об/мин за 30 сек. Считая угловое ускорение шпинделя во время пуска постоянным, определить число оборотов шшшделя за время пуска. Найти скорость и ускорение точки на поверхности блочка шпинделя при дальнейшем равномерном вращении, если его диаметр равен 40 мм. Решение. Величина угловой скорости нтин-деля во время пуска растет пропорционально времени u) - e.t и достигает значения 15 000 об/мин через 30 сек. Определяем величину углового ускорения Ш1шпделя 15 000-2:; 50 . :-=-. = 52,4 сек\ Угол поворота ншинделя за время пуска определится по формуле (8*) при ш„ = 0 и ср = 0: е<2 9 = -у: 50- 30= = 7500л радиан. Число оборотов за время пуска будет: = -- = 3/50 оборотов. 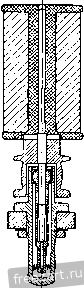 2л К задаче 4.5. Модуль скорости точки на ободе блочка шпинделя (после достижения рабочей скорости) равен г) = шг=15 000-20= 10 000- mm/cckIQik м/сек = 3\,4 м/сек. Ускорение этой точки при дальнейшем равномерном вращении будет состоять только из нормального ускорения, величина которого найдется по формуле 15 000-27:>2 20 , 5 2 / 9 -я - -\-да--] що м/сек-=И000к' м/сек\ W = W = (1) г = Это ускорение направлено но перпендикуляру, опущенному из точки на ось вращения. е и высоту подъема <Pi = -г)- = 0,8 рад /21 = ср,4- = 0.32 м. На втором этапе величина скорости лифта постоянна и определяется равенством (2). Следовательно, высота подъема за этот этан будет; , = 11,(3 -,) = 0,32. 16 = 5,12 м. Задача 4-6- При подъеме лифта угловое ускорение барабана диаметром cf = 0,8 м, на который наматывается канат, поднимающий клеть, изменяется соглас- ce/i по показанному на ри- сунке графику. Определить наиболь-шую скорость подъема -ccert лифта, а также высоту подъема за 20 сек. Решение. Движение лифта распадается па К задаче 4.6. три этапа. В течение первых двух секунд барабан, начиная движение из состояния покоя, вращается с постоянным угловым ускорением. Следовательно, величина его угловой скорости равна а угол поворота определяется по формуле Полагая t = 2 сек, находим модуль угловой скорости в конце первого этапа движения ( 1 = 0,4.2=0,8 сел-- и величину скорости точки на поверхности барабана, равную модулю скорости, с которой наматывается канат и поднимается лифт в этот момент времени, iij=u)ir = 0,8-0,4 = 0,32 MJccK. (2) Это и будет наибольшая скорость подъема, так как на втором, следующем, этапе угловое ускорение равно нулю, угловая скорость барабана остается неизменной и, следовательно, скорость подъема лифта сохраняет свою величину. Определим путь, пройденный лифтом в течение первых двух секунд. Для этого находим из (1) угол поворота барабана за это время На третьем этапе вращение барабана происходит с постоянным угловым замедлением. Следовательно, угол поворота будет равен <Рз = ~ /.i) - J- = 0,8 . 2 - = 0,8 рад. Теперь легко }1айти высоту подъема лифта на этом этане: /;з = 9зу =0,8. 0,4 = 0,32 м. Таким образом, полная высота подъема лифта /; = hi -{- hi -f /гд = 5,76 м. Задача 4.7. Вал с присосдипеппыми к нему пластинами вращается в подщипииках согласно уравнению 9 = aln(l+V.V где 9 - угол поворота вала, а и Шо - постоянные коэффициегтги. Определить угловую скорость и угловое ускорение вала. Найти скорость и ускорение центра пластины Л, отстояи1его иа расстоянии R от оси вращения. Решение. Проекция угловой скорости вала на ось врамгеьшя равна первой производной от угла ноиорота по времени 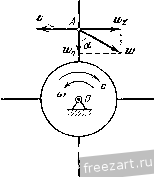 Из этого равенства видно, что в пачаль-1П.1Й момент при = 0 величина угловой скорости вала равнялась ш - Опре- к; задаче 4.7. деляем проекцию углового ускорения вала иа ось вращения как производную от угловой скорости по времени а или, сопоставляя (2) и (1), Проекция углового ускорения отрицательна, проекция угловой скорости вала с течением времени неограниченно уменьшается. Переходим к определению скорости и ускорения центра А пластины. Модуль скорости этой точки равен а Ускорение этой точки складывается из нормального и касательного ускорений. Величина нормального ускорения Wn =- R - = Проекция ускорения на касательную определяется формулой Модуль полного ускорения а Угол а, составляемый ускорением точки с радиусом, соединяющим ее с осью вращения, находится из уравнения t а = = - Направления скорости и ускорения центра пластины изображены на рисунке. Отрицательное значение tga указывает на то, что угол а откладывается в сторону, противополомс-ную направлению вращения твердого тела. Задача 4.8. Ускорение любой точки вала, вращающегося в подшипниках, составляет постоянный угол 60° с перпендикуляром, опущенным из этой точки иа (кь вала. Начальное значение проекции угловой скорости на ось z, направленнсй 1Ю оси вала, равно - начальный угол [юворота вала равен нулю. Определить касательное, нормальное п полное ускорения точки вала, расстояние которой от осп вращения г. Найти урав-neinie вращения пала вокруг неподвижной оси, а так>;е зависимость величины угловой скорости от угла поворота вала. Решение. Угол а между ускорением точки и перпендикуляром, опущенным из точки на ось вала, связан с проекцией углового 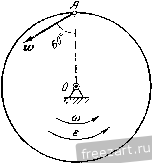 К задаче 4.8. --(4) Далее, из (1) и (4) определяем проекцию углового ускорения вала па ось вращения = tg а 0)1 = Кз-. Проекция ускорения точки, радиус вращения которой г, на направление касательной определяется формулой У^ ru>i = =---7-. Модуль нормального ускорения этой точки (1+ /30* Тогда величина полного ускорения точки Для нахождения уравнения движения вала воспользуемся равенством (4), записав его так: Jjf---- о . /54 ускорения и величиной угловой скорости соотношением Подставляя значение tga и учитывая, что t - -, имеем: Уш=.;. (2) Переменные отделены. Интегрируя, находим: Vst-+c. (3) где С-произвольная постоянная интегрирования. Определяем ее, подставляя в равенство (3) начальные условия: ш^ = -ш^ нрн = 0, откуда С- - и, следовательно. Умножая обе части рав(?нства (5) на dt, отделяем неременные: Интегрируя, имеем: 0 Vt Q==--In(I+o) l/30. Произвольная постоянная интегрирования Q определяется путем подстановки в уравнение (6) начальных данных: при = 0 <р = 0. Эю дает Ci=0. Следовательно, 3 1 + ио Это и есть уравнение вращения вала. Переходим к определению зависимости проекции угловой скорости на ось вращения от угла поворота. Для этого умножим обе части равенства (2) на rf<p. Находим: ojJ dt co Интегрируя, имеем: 1/з<р = 1пС.шг, 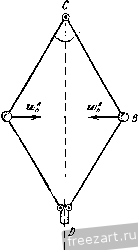 или Произвольную постоянную интегрирования d определяем, подставляя начальные данные: при^ = 0<р = 0 и (1)= -ш„. Тогда С.1 =--и окончательно находим: = - ш^е^ч. Задача 4-9. Регулятор Уатта вращается с постоянной угловой скоростью О) во-К задаче 4.9. круг вертикальной оси. Угол АСВ при этом оказался равен 60°, а ускорение шаров А и В равно но величине lOOg, где = 980 см/сек'. Стержни АС, ВС, AD и ВО одинаковой длины /=10 си/. Сколько оборотов в минуту делает регулятор? Решение. Для того чюбы найти величину угловой скорости регулятора, напишем зависимость ускорения шаров от параметров регулятора. Так как регулпор вращается с постоянной угловой скоростью, то ускорение шара будет нормальным ускорением, модуль которого определяется формулой = гш == / sin 30°ш^ где г - кратчайшее расстояние шара до оси вращения. С другой стороны, согласно условию Приравнивая эти два выражения нормального ускоре1тя шара, находим: , в технической системе единиц угловая скорость регулятора будет ,чдп п и = ш об\мпн = --jy- = 1340 об/мин. Для приобретения навыков в решении задач на вращение твердого тела вокруг неподвижной оси рекомендуется решить следующие задачи нз Сборника задач но теоретической механике* И. В. Мещерского, издания 1950 г. и более поздних лет: 375, 376, 382, 385, 386, 388, 390, 393. § 2. Преобразование простейших движений Под преобразованием npocretiunix движений следует понимать: а) преобразование вращательного дкижепия в ноступатсльпос (н обратное преобразование), б) преобразование вращения вокруг одной неподвижной оси во вра-шетше вокруг другой неподвижной оси и в) преобразование одного по-пупательного движения в другое поступательное движение. При решении задач о движении механизмов, иреобразую1них нростейише движения, следует пользоваться соимсстно формулами кинематики точки н формулами кинематики твердого тела, вращающегося вокруг неподвижной оси. Преобразование вращения одного твердого тела вокруг неподвижной оси во вращение второго твердого тела вокруг другой неподвижной оси осуществляется посредством зубчатого или фрикцнотшого зацепления двух колес (рис. 4.3, а, б) и.ти при помощи ременной передачи (рис. 4.4, 4.5). 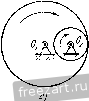 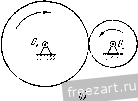 Рис. 4.3. 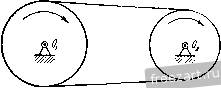 Рис. 4.4. При внутреннем зацеплении (рис. 4.3, а) и пескрещивающейся ременной передаче (рис. 4.4) направление вращений обоих колес совпадает. При внешнем зацеплении (рис. 4.3, б) н скрещивающейся ременной передаче (рис. 4.5) направление вращения колес противоположно. Величины скоростей па ободе зубчатых колес, находящихся в зацеплении, равны. Так>1-;е равны по модулю скорости на ободе шкивов ременной передачи, если нет скольжения ремня по шкиву. Угловые скорости колес обратно пропорциональны числам зубцов или радиусам, или диаметрам л .££ (I*) а г, г, (/, в этой формуле Ш], (flj - модули- угловых скоростей, г г.2 - радиусы начальных окружностей, di, d, - диаметры начальных окружностей, 2], Z.J - числа зубцов первого и соответственно второго колеса. Зубчатые колеса и ременные передачи, изображенные на рис. 4.3 - 4.5, представляют примеры последовательного соединения колес и шкивов. При последовательном соединении каждое из колес вращается вокруг своей неподвижной оси. Часто применяется параллельное соединение колес, когда два колеса вращаются вокруг одной неподвижной осн. Если при этом они жестко соединены друг с другом, то их угловые скорости равны. При решении задач на преобразование простейших движений рекомендуется такая последовательность действий: 1) исходя из условия задачи, выписать уравиепие движения или другие кинематические соотношения для того твердого тела, движение которого известно; 2) пользуясь формулами кинематики точки и кинематики вращения твердого тела вокруг неподвижной оси, найти урапнение движения другого твердого тела, которому передается движение, а также найти скорости и ускорения различных точек этого твердого тела. Задача 4.10. Зубчатое колесо / находится во внешнем зацеплении с зубчатым колесом . Первое колесо имеет диаметр Di = 400 мм и вращается с угловой скоростью (fljTt се/с вокруг неподвижной оси Oj. 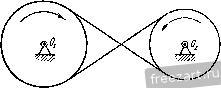 Рис. 4.5. Определить угловую скорость второго колеса, если его диаметр равен Dss = 320 мм и оно вращается вокруг неподвижной оси 0.. Решение. В месте соприкосновения зубцов обоих колес скорости точек первого и второго колес одинаковы. Обозначая величину этой скорости V, имеем: и, следовательно, 7). Пользуясь формулой (1), находим: co.d, г. 400 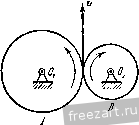 = -j-ic сек К задачи 4.10. Так как колеса находятся во внешнем зацеплении, то их угловые скорости направлены в противоположные стороны. Если колесо / вращается против часовой стрелки, то колесо вращается по часовой стрелке. Задача 4.11. Зубчатое колесо / находится во виутрением зацеплении с зубчатым колесом . Радиус первого колеса ri=I50 мм и оно делает ni = -- 1500 об/мпн, вращаясь вокру!- неподвижной оси Oi. Определить радиус второго колеса, если оно должно вращаться вокруг неподвижной оси Oi, делая n.j = 4500 об/мин. Решение. В месте соприкосновения зубчатых колес скорости точек первого и второго колес должны быть равны. Величина скорости точки обода колеса / равна 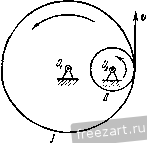 К задаче 4.11. Модуль скорости точки обода колеса равен Сопоставляя равенства (1) и (2), находим: Га < 1 1 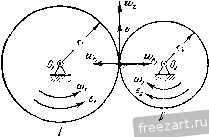 К за.таме 4.12. Так как величины угловых скоростей пропорциональны числам оборотов в минуту, имеем: п. 1500 = 7.7=°-4500 =0 В рассматриваемом случае внутреннего зацепления оба зубчатых колеса вращаются в одну сторону. Задача 4.12. Зубчатое колесо /, радиус которого равен Гу, находится во внешнем зацеп.чении с зубчатым колесом радиуса г^. Первое колесо вращается в данный момент с угловой скоростью О] и угловым ускорением 8,. Определить угловую скорость и угловое ускорение второго колеса, а также нормальное ускорение находящихся в соприкосновении точек колес. Решение. При вращении зубчатых колес, находящихся в зацеплеини, скорости точек соприкосновения обоих колес должны быть равны в любой момент времени. Для этого необходимо, чтобы были равны пе только скорости этих точек, но и их касательные ускорения, ибо если в данный момент скорости этих точе1с равны, а касательные ускорения не равны, то в следующий момент времени нарушится и равенство скоростей точек соприкосновения. Из равенства людулсИ скоростей вытекает соотношение <0.2=U),Ii. (1) Угловая скорость второго колеса o,j при внешнем зацеплении направлена в сторону, противоположную угловой скорости <а, первого колеса. Величины касательных ускорений т очек соприкосновения обоих колес будут: \w,i\--=r,e ; I = r.jei. Приравнивая эти значения, получаем: что легко найти также непосредственно путем дифференцирования соотношения (1). Угловое ускорение второго колеса е. направлено в сторону, противо-но.тожную угловому ускорению е, первого колеса. 1 ... 25 26 27 28 29 30 31 ... 51 |
 |
 |