

 |
 |
|
Навигация
|
Главная » Мануалы § 10. Аналитический способ определения равнодействующей сходящихся сил на плоскости. Уравнения равновесия сил Равнодействующая R сходящихся сил Pj, Pj. метрической сумме сил (рис. 30): Р„ равна гео- Из векторной алгебры известно, что проекция геометрической суммы векторов на любую ось равна алгебраической сумме проекций составляющих векторов на ту же ось. Таким образом, проекции к и у равнодействующей силы R определяются по формулам: K = Ki ++ ...+к„. I (10.1) где , = P,cos(Pi. i); 2 = P2Cos(P2, i); A,=>;cos(p;, i); K, = PiCos(Pp j); K2 = P2Cos(P2, i);
Рис. 30. K = P COS (P . j). Формулам (10.1) можно придать вид А'= 2;. (10.2) где 2- знак суммирования, а 2.....п. Вычислив проекции равнодействующей X и Y, найдем модуль а направление равнодействующей по формулам (9.3): Я = УА2 4-К2 ; cos(R. 0==: cos(R, j)=. Если сходящиеся силы уравновешиваются, то R = ]/АГ2 4- К2 = о, т. е. А' = О и К = 0. В этом случае имеем два следующих уравнения равновесия сил: S.-.o, 1 =0. При помощи этих уравнений можно решать задачи на равновесие (Ю.3> у 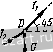 сходящихся сил, если число неизвестных величин в задаче равно двум. Такой метод решения этих задач называется аналитическим. Если в задаче на равновесие сходящихся сил число неизвестных превышает два, то ее нельзя решить методами статики твердого тела. Методы решения таких задач излагаются в курсе сопротивления материалов. Пример 6. Решить пример 3 (рис. 24а) аналитическим способом [при помощи уравнений равновесия (10.3)]. 1 t PemeifHe. Воспользуемся уравне- j---- [ ниями равновесия сходящихся сил, при- ложенных к каждому из узлов D vi А. Покажем на схеме (рис. 31) все силы, приложенные к этим узлам, как известные, так и неизвестные. Направления реакций столба АВ и подкоса АС не известны. Условимся эти стержни считать растянутыми и направим их реакции Si и S2 от узла. Ответ со знаком минус укажет, что соответствующий стержень не растянут, а сжат. Проведем оси координат, направив их по горизонтали и вертикали. Составим суммы проекций всех сил, приложенных к узлу D, ш оси х и 3 и приравняем эти суммы нулю: 2- = 0; 7 iCos45° -72cos30° = 0. 2г=0; 7 iCos45° -ТзСозбО -G = 0. Вычитая второе уравнение из первого, найдем: - Г2 cos 30° + Гг cos 60° -f О = О, G 518 \ с ~В Рис. 31. 2 ~~ cos 30° - cos 60° ~ 0,866 - 0,5 Из первого уравнения определим Tj: = 1414 н. Га COS 30° 1414. 0,866 = 1732 . cos 45° 0,707 Составим уравнения равновесия сил, приложенных к узлу А, учитывая, что Г2 = 72= 1414 н: 2г==0; - 52 cos 60° +Гг cos 30° = 0. 2К;=0; - S2cos30° -Si + r2cos60° = 0. Из первого уравнения: .30° 1414.0,866 52 = - cos 30° cos 60° -=2449 й. Из второго уравнения Sj = - S cos 30° + cos 60° = = - 2449 0,866+ 1414 0,5 = -1414 н. Так как 52 =+2449 н, то условно принятое направление силы S2 совпадает с действительным, т. е. подкос АС растянут. Ответ Si = -1414 н показывает, что условно принятое направление силы Si противоположно действительному, т. е. столб АВ не растянут, а сжат. Примечание. Схема, по которой составлены уравнения равновесия (рис. 31) не изменяется, хотя направления некоторых сил на ней и противоположны действительным (Si). Числовые значения полученных из уравнений равновесия величин определяют модули сил, а их знаки - их направления. Истинное направление сил определяют по схеме н по знаку ответа. § П. Определение усилий в стержнях плоских ферм по способу вырезания узлов. Леммы о пулевых стержнях Фермой называется геометрически неизменяемая шарнирно-стерж-невая конструкция (рис. 32). BepxHi/u пояс 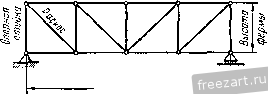 Нижний пояс Пролет фермы Рис. 32. Если оси всех стержней фермы лежат в одной плоскости, то ее называют плоской фермой. Точки, в которых сходятся оси стержней, называются узлами фермы, а те узлы, которыми ферма опирается на основание, называются опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс, а расположенные по нижнему контуру - нижний пояс фермы. Вертикальные стержни называются стойками, а наклонные- раскосами. На рис. 33, 34 и 35 изображены стержневые опоры фермы. Реакция каждого из опорных стержней, очевидно, направлена по оси этого стержня. Если шарниры, соединяющие стержни фермы, предполагаются идеальными, т. е. без трения, а все внешние силы - приложенными Опорный шершни к узлам фермы, то все стержни испытывают лишь растяжение или сжатие, так как к каждому стержню приложены силы только на его концах * Реальные фермы не имеют идеальных шарниров, однако такое допущение облегчает вычисление усилий в стержнях фермы, а результаты вычислений при этом допущении вполне пригодны для практики. Рассмотрим определение усилий в стержнях фермы по способу вырезания узлов Этот способ состоит в том, что мысленно вырезают узлы фермы, прикладывают к ним соответствующие внешние силы и реакции стержней и составляют по два уравнения равновесия сил, приложенных к каждому узлу. Так как в начале расчета фермы не известно, какие стержни фермы растянуты и какие сжаты, то условно предполагают, что все стержни растянуты (реакции стержней направлены от узлов) Если в результате вычислений получают ответ со знаком минус, то соответствующий стержень сжат 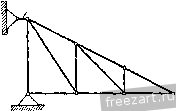 Рис 33 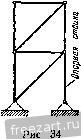 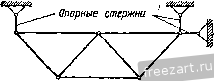 Рис 35 Найденные реакции стержней равны по модулю внутренним усилиям в стержнях (§ 3). Последовательность рассмотрения узлов определяется обычно тем, чтобы число неизвестных сил, приложенных к узлу, не превышало двух. Тогда эти неизвестные определяются сразу из двух уравнений равновесия сил, действующих на этот узел. Чтобы убедиться в правильности произведенных вычислений, для сил, приложенных к каждому узлу, можно построить многоугольник, который должен быть замкнут. Определим по способу вырезания узлов усилия в стержнях фермы, изображенной на рис. 36, а. Если сила Р = 60кн, приложен- *) Веса стержней достаточно малы по сравнению с силами, приложенными в узлах фермы, поэтому ими обычно пренебрегают. ная к узлу Е фермы, вертикальна и реакция шарнирно-подвижной опоры В, перпендикулярная к опорной плоскости, тоже вертикальна, то линия действия реакции шарнирно-иеподвижиой опоры А должна быть им параллельна, т. е. должна быть тоже вертикальна (примечание к § 7). С f 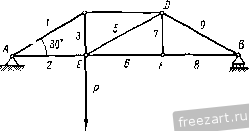 Рис 36а. Из элементарного курса физики известно, что силу Р можно разложить на две, параллельные ей составляющие силы, приложенные в точках А VI В Модули этих составляющих сил обратно пропорциональны расстояниям АЕ и BE, а сумма их равна модулю силы Р Этим силам, представляющим собой давление фермы на Узе/1 А
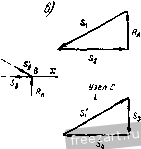 Узел£ Узел 8 Рис. Ш,б, в. опоры, соответствует равное по модулю противодействие в виде реакций опор, которые определятся по следующим формулам: /?л = 40 кн Rj, = 20 кн. Составим по два уравнения равновесия сил, приложенных к каждому из узлов фермы (рис. 36,6) и для проверки правильности произведенных вычислений построим многоугольники сил, которые должны быть замкнутыми. При построении многоугольников все силы отложим в некотором масштабе по их истинным направлениям, соответствующим растяжению или сжатию, руководствуясь результатами вычислений (рис. 36,8). Расчет начнем с узла А, к которому приложены лишь две неизвестные силы Sj, и S2. Узел А 2г = 0; 52 + 5iCOs30° = 0; 2Кг=0; Р^+ 5, cos 60° = 0; Sj = - = - 80 кн; = - Sj cos 30° = 69,2 кн. Узел С Xi = 0; - 5lcos30°+S4 = 0; 2k;=0; - sIcos60° -5з = 0; 5з =! - 5l cos 60° = 40 kh; S4 = S[ cos 30° = - 69,2 кн. Узел E 2a; = 0; - 52-bS6 + S5Cos30°=ro; 2k;=0; S3 -P--S5cos60°.5=0; p - s S5 = - == 40 kh; Se = S2 - S5 cos 30° = 34.6 >сн. Узел F 2f = 0; -S6 + S8 = 0; S8==S6 = 34,6 кн; 2k, =0; S7 = 0. Узел В К, = 0; P-}-S9Cos60° = 0; S = --3 = -40 кя- Таблица 1 Таблица усилий
Приведенная таблица показывает, что верхний пояс фермы сжат, нижний - растянут. Усилия в отдельных стержнях загруженной фермы могут оказаться равными нулю. Такие стрежни фермы принято называть нулевыми стержнями. Рассмотрим леммы, пользуясь которыми можно определить нулевые стержни, не производя расчета фермы. Лемма 1. Если в незагруженном узле фермы сходятся два стержня, то усилия в этих стержнях равны нулю (рис. 37). 2: = 0; S2-4-5iCosa=:0; 2К; = 0; 5i cos (90° - а) = 0;  62 = 0. Рис. 37. Лемма 2. Если в незагруженном узле фермы сходятся три стержня, из которых два расположены на одной прямой, то усилие в третьем стержне равно нулю. Усилия в первых двух стержнях равны между собой (рис. 38), 2; = 0; -i + Sj + SgCOsaO; 2К~0; 5зсов(90° -а) = 0; 5з = О и 5i = S2. Лемма 3. Если в узле фермы Рис. 38 сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадаещ с осью одного из стержней, то усилие в атом стержне равно по модулю приложенной силе, а усилие в другом стержне равно нулю (рис. 39). 2, = 0; 5icosa = 0; Si==0. 2К; = 0; -P~S2 + SiSina = 0; S2 = -P. Пример 7. Применить леммы о нулевых стержнях к определению незагруженных стержней ферм, изображенных вместе с действующими на них внешними силами и реакциями опор (рис. 40-44). Применяя лемму 2 к узлу / фермы, изображенной на рис. 40, устанавливаем, что 5з = 0. Далее, мысленно отбрасывая стержень 3, применяем эту же лемму к узлу и находим, что 55 = 0. Рассматривая ферму, изображенную на рис. 41, применяем лемму 1 к узлу / и заключаем, что Sj =0 и 2 = 0. Затем применяем лемму 3 к узлу и устанавливаем, что S - 0. На рис. 42 рассматриваем узлы /, II, III и находим: ЗцО, 59 = 0. 5з = 0. Рассматривая узлы I к II (рис. 43), можно заключить, что = О и 59 = 0. 3 А. А. Яблонский 5г Рис. 39. /8 в
Рис. 40. 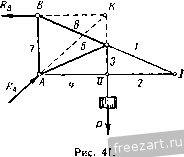
Рис. 42.
Рис. 44. рассматривая последовательно узлы /-VII фермы, изображенной на рис. 44, находим: 5j5 = 0; 5i3 = 0; = 0; S = 0; S=Q; S=Q; S = 0. Вопросы для самоконтроля 1. Что называется связью? В чем заключается принцип освобождаемости от связей? 2у Перечислите основные типы опор, для которых линии действия реак-Ц) известны. 3. Как направлена реакция опорного шарнира, если твердое тело соединено с опорой при помощи стержня, имеющего на концах шарниры? 4. Как определяется направление равнодействующей системы сходящихся сил при построении силового многоугольника? 5. Каковы условия н уравнения равновесия плоской системы сходящихся 6. Как формулируется план решения задач статики па равновесие сил? 7. При каком условии три непараллельные силы, приложенные к твердому телу, уравновешиваются? 8. В чем заключается сущность способа вырезания узлов? 9. Каковы леммы о нулевых стержнях? ГЛАВА III ТЕОРИЯ tlAP СИЛ, ЛЕЖАЩИХ В ОДНОЙ ПЛОСКОСТИ § 12. Момент силы относительно точки на плоскости Моментом силы относительно некоторой точки на плоскости называется произведение модуля силы на ее плечо относительно этой точки, взятое со знаком плюс или минус (рис. 45): Mo=±Pd. (12.1) Плечом силы Р относительно точки О называют длину перпендикуляра, опущенного из точки О на линию действия силы; точка О называется центром момента. Момент силы относительно точки будем считать положительным, если сила Р стремится повернуть плоскость чертежа вокруг точки О в сторону, противоположную движению часовой стрелки, и отрицательным - в обратном случае. Момент силы Р относительно точки О численно равен удвоенной площади треугольника ЛОВ Мо=± 2ДЛ0В, где А и В - начало и конец силы, а О-центр момента. Если линия действия силы проходит через точку, т. е. d= О, то момент силы относительно этой точки равен нулю. Единица момента равна произведению единицы силы на единицу длины. 3* 35 Если сила выражена в ньютонах, а плечо в метрах, то момент силы выражается в ньютон-метрах (к м). В том случае, если к телу приложено несколько сил, лежащих в одной плоскости, можно вычислить сумму моментов этих сил относительно какой-либо точки О в этой же плоскости (рис. 46): и т. д. 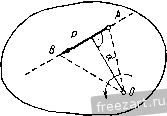 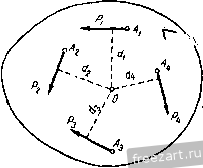 Рис. 45. Рис. 46. Момент Mq, равный алгебраической сумме моментов данной системы сил относительно какой-либо точки в той же плоскости, называют главным моментом системы сил относительно этой точки: § 13. Пара сил. Теорема о моменте пары Из элементарного курса физики известно, что равнодействующая R двух параллельных сил Pj и Pj одного направления (рис. 47,а) имеет 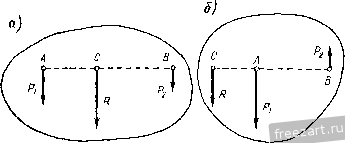 Рис. 47. такое же направление, а ее модуль равен сумме модулей слагаемых сил. Точка С приложения равнодействующей делит отрезок между точками приложения сил Л и В на части, обратно пропорциональ- 1 2 3 4 5 6 ... 44 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |