Промышленное охлаждение - freezart.ru. Схемы и периодика

Главная » Мануалы

1 2 3 4 5 6 7 ... 51

ющей R активных сил Р ц F должна проходить через точки О и В, т. е. должна составлять с вертикалью угол OBD, который мы обозначим через р. Учтя, что вес Р приложен в середине стержня, получим

АС=СВ. При этом АО =00. Так как tga= - = , tgp = 0D

Построив на рис. б равнодействующую R активных сил Р и F под углом р к вертикали, найдем из прямоугольного треугольника KLM:

При выполнении этого условия стержень АВ будет находиться в рав-р

новесии. Если Figi, то стержень опрокинется вокруг шарнира В

в направлении по часовой стрелке, если же F<C-2g* то против часовой, стрелки.

Данную задачу проще всего решить, применив условие равновесия рычага (П*), которое здесь имеет вид

тд(Р)-\-,Пд{Р) = 0. (1)

Так как

тв{Р) = Р-ВЕ=]Р-АВ sin х, {F) = - F BD= - F АВ cos а, то, подставив эти значения в формулу (1), получим;

уР-ЛВ sin а -F-ScosaO,

Рекомендуем решить следующие задачи из Сборника задач по теоретической механике И. В. Мещерского, издания 1950 г. и последующих лет; 62, 63, 64.

§ 2. Произвольная плоская система сил. Случай параллельных сил

Р. Равновесие твердого тела при наличии плоской системы сил. Напомним сначала, что равнодействующая двух параллельных сил, направленных в одну сторону, равна по модулю сумме модулей данных сил и направлена в ту же сторону. Линия

действия равнодействующей делит внутренним образом расстояние между линиями действия данных сил на части, обратно пропорциональные этим силам. Таким образом (рис. 1.25),

Равнодействующая двух параллельных сил, пе равных по модулю (пусть IFflFil) и направле1П1ых в разные стороны, равна по модулю разности модулей этих сил и направлена в сторону большей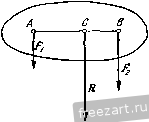


	в

Рис. 1.25.

Рис. 1.26.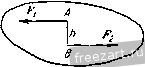

силы. Линия действия равнодействующей делит внеш1тм образом расстояние между линиями действия д^шых сил на части, обратно

пропорциональные этим силам. Таким образом (рис. 1.26),

P-F F- Ft ВС

Система двух параллельных сил, равных по модулю и направленных в разные Рис. 1.27. стороны, называется й^ой сил (рис. 1.27).

Расстояние между линиями действия этих сил называется плечом пары. Так как две силы, равные по модулю и направленные в разные стороны, не лежат на одной линии действия, то твердое тело, к которому приложена пара сил, не находится в равновесии. Пара сил стремится повернуть твердое тело, к которому она приложена.

Мерой действия пары сил является алгебраическая величина, называемая ее моментом. Момент пары сил равен по абсолютной величине произведению модуля одной из сил пары на плечо. Если пара сил видна направленной против часовой стрелки, то момент пары положителен, если по часовой стрелке, то отрицателен. Примеры даны на рис. 1.28.

Теория пар сил на плоскости сводится к четырем теоремам.

Теорема 1. Алгебраическая сумма моментов сил, составляющих пару, относительно произвольной точки плоскости не зависит от выбора этой точки и равна моменту пары.

Теорема 2. Не нарушая состояния твердого тела, пару сил можно переносить в плоскости ее действия.

Теорема 3. Пары сил, моменты которых равны, эквивалентны. (Пары сил называются эквивалентными, если одну из пар можно за-MeiHiTb другой, не нарушая состояния твердого тела.)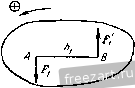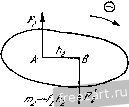

Рнс. 1.28.

Это значит, что, не нарушая состояния твердого тела, можно изменять величину плеча либо величину силы, сохраняя при этом неизменным момент пары сил (рис. 1.29).

Рис. 1.29.

Теорема 4 (сложение пар сил на плоскости). При сложегши нескольких пар сил на плоскости получается равнодействующая пара, момент которой т равен сумме моментов слагаемых пар:

/я=:/я, + /Яз + ...4-/я = 2 /я=г 2 ±.PkK-

ft=I ft=l

На рис. 1.30, а показаны три пары сил с моментами mi = Fihi, т<1 = - Fhi, тз = Рфз, а на рис. 1.30,6 представлена их равнодействующая пара с моментом т == Ефх - Рф -~- Fh = Fh.

Для рав1ювесия твердого тела под действием нар сил, лежащих в одной плоскости, необходимо и достаточно, чтобы сумма моментов данных пар равнялась нулю:

] /йй = 0, X. е. 2=нР,/г, = 0. ft=i ft.= i

Приведение силы к данной точке. При приведении силы к данной точке добавляется присоединенная пара сил, момент которой равен моменту данной силы относительно центра приведения.

Рис. \Ж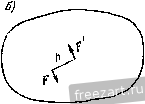

Это значит, что, не нарушая состоя1шя твердого тела, можно силу F приложить в точке В (рис. 1.31), добавив присоединенную пару сил, момент которой равен моменту зада1гиой силы F относительно центра приведения В.

Приведением силы к данной точке широко пользуются при преобразовании произвольной плосгсой системы сил к простейшему виду.

Елаеным вектором V называется векторная сумма сил, приложешгых к твердому телу, т. е.

V=E Р..

к = I

Проекции главного вектора и V, па оси декартовых координат равны сумма.м проекций даггных сил на соответствующие оси: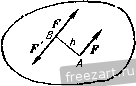

Рис. 1.31.

Vx= Fk., Vy= F,y.

Модуль главного вектора

v=Vvi+v}.

Направляющие косинусы главного вектора определяются по формулам:

cos (хГу) = , cos ivTv) = .

Главным моментом mQ относительно цег1тра О называется сумма моментов сил, приложенных к твердому телу, относительно этого

В соответствии с определением главный вектор V является статическим инвариантом, т. е. величина и направление главного вектора не зависят от выбора центра приведения системы. Главный момент системы при перемене центра, вообще говоря, меняется. Главный момент /Яд плоской системы сил относительно нового центра приведения А равен сумме главного момента этой системы сил относительно старого центра О и момента относительно нового центра А главного вектора V, приложенного в старом центре О:

л = о + д(о)-

Приведение к одному центру сил, произвольно расположенных ira плоскости. В результате приведения сил, произвольно расположенных на плоскости, к одному центру О система сил преобразуется к и])иложенной в этом центре силе, равной 1-лавному вектору V, и паре сил, момент которой равен главному моменту /Яд.

Не следует отождествлять силу V с равнодействующей Ц, так как равнодействующая - это одна сила, которая эквивалентна данной системе сил, а сила V эквивалентна данной системе сил только в совокупности с парой сил, момент которой равен главному моменту /Яд.

Частные случаи приведения сил, произвольно расположенных на плоскости, а) Главный вектор равегг нулю, но главный момент не равен нулю, т. е. V=0, т^О. Система сил приводится к паре сил, момент которой равен главному моменгу /Яд (в этом случае главный момент системы сил не зависит от выбора центра приведения).

б) Главный вектор не равен нулю, но главный момент равен нулю, т. е. V 9 О, /Яд=0. Система сил приводится к равнодействующей R= V, приложенной в центре приведения системы.

в) Главный вектор и главный момент системы не равны нулю, т. е. V 9 О, niQ 0. Система сил приводится к равнодействующей R=V, линия действия которой отстоит от линии действия силы V на расстоянии h = mQ/V. Положение линии действия равнодействующей R должно быть таким, чтобы знак момента равнодействующей R относительно центра приведения О совпадал со знаком главного момента системы сил /я относительно центра О.

Сила V и равнодействующая R равны по модулю и параллельны (рис. 1.32).

Теорема Вариньона для произвольной плоской системы сил. Если система сил приводится к равнодействующей.

центра, т. е.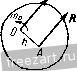

г) Главный вектор V и главный момент /Яд системы равны нулю V=0, т^ - О. Твердое тело, Рпс. 1.32. которому приложена да1Н1ая система сил, нахо-

дится в равновесии. Уравнения равновесия твердого тела под действием нроизвольнойплоской системы сил. Для равновесия твердого тела иод действием произгюльной плоской системы сил fieo6xoflHMo и достаточно, чтобы су.м.ма проекций всех сил rfa произвольно выбрагшые оси декарговых координат л: и у и сумма моментов этих сил относительно произвольно выбранной точки О равнялись нулю;

л - I Д! = I ft = 1

В случае произвольной плоской системы сил задача является статически определенной, если число алгебраических неизвестных не более трех.

Можно ограничиться состанле1щем одного урав1юния проекций, например на ось х, но при этом составить два уравнения моме1ггов относительно двух произвольных точек;

Рк. = 0, ;niF,) = Q, j]maiF,) = 0. (2*)

При этом следует иметь в виду, чго ось, относительно которой составляется уравнение проекций, не должна быть расположена перпендикулярно к прямой, проходящей через две точки, опгосительно которых составляются уравнения моментов. Если это условие не будет выполнено, то уравнение проекций окажется следствием уравнений моментов и решение подобной системы уравнений равновесия даст возможность определить только две неизвестные величины вместо трех.

Можно, минуя составление уравнений проекций сил, составить три уравне1шя моментов относительно трех произвольно выбранных точек:

Е л С *)=0 Е в (k)=0. Е с с'/)=о- (2*)

Л=1 ftl ft=l

то момент равнодействующей относительно произвольной точки ранен сумме моментов данных сил относитель}го той же точки (теорема у Вариньона):

При ЭТОМ следует иметь а виду, что эти три точки не должны лежать на одной прямой, так как иначе одно из уравнений равновесия окажется следствием двух других.

Уравнения равновесия твердого тела под действием плоской системы параллельных сил имеют вид

S F,x=0. 2 о(П) = 0, (4*)

k=l A=l

причем ось X не перпендикулярна данным снла.м. Задача является статически определенной, если число алгебраических неизвестных не более двух.

Можно обойтись без уравнений проекций и составить два уравнения моментов относительно двух произвольно выбранных точек:

i] (Pk) = 0, S (Ffc) = 0. (5*)

Следует иметь в виду, что эти две точки не должны лежать на прямой, параллельной данным силам, так как в противном случае одно из уравнений равновесия окажется следствием другого.

При решении задач на равновесие твердого тела, к которому приложена плоская система параллельных сил, надо выполнить четыре первых пункта, указанных в начале кннги на стр. 15. Затем:

5) убедиться в том, что данная задача является статически определенной, т. е. число алгебраических неизвестных величин не более двух;

6) выбрать систему осей декартовых координат;

7) составить уравнения равновесия системы параллельных сил;

8) решив уравнения равновесия, определить неизвестные величины.

Если величина какой-либо неизвестной силы окажется отрицательной, то это означает, что направление этой силы противоположно тому, которое было изображено на рисунке.

Оси декартовых координат целесообразно направлять так, чтобы одна из них оказалась параллельной всем силам, приложенным к твердому телу. Уравнение моментов рекомендуется составлять относительно точки, лежащей на линии действия неизвестной силы. Это дает возможность определить одну из неизвестных величин непосредственно из уравнения моментов.

При решении задачи с помощью двух уравнений моментов шестой пункт решения задачи отпадает. При этом не следует забывать, что точки, относительно которых составляются уравнения моментов, не должны лежать на прямой, параллельной силам.

7777777, 77у

2a a)

Задача 1.12. В кузове грузовой автомашины весом Р лежит груз D весом d - Pll.

Пренебрегая силами трения, определить давления передних и задних колес автомашины на шоссе. Размеры указаны иа рис. а, С - центр тяжести автомашины.

Решение. Рассмотрим равновесие автомашины. К ней приложены активные силы: Р - вес автомашины, Q - вес груза. Применив закон освобождаемости от связей, мысленно отбросим связь - шоссе. Реакции шоссе /?д и приложе1шые к колесам, при отсутствии трения направлеггы перпендикулярно к шоссе, т. е. вертикально вверх (рис. б). Конечно, Rf и R являются суммарными реакциями соответственно

двух задних и двух передних колес. Итак, автомашина находится в равновесии под действием плоской системы параллельных сил: Р, Q, /?д и R. Задача является статически определенной, ибо число алгебраических неизвестных равно двум.

Направим ось х параллельно силам вертикально вверх, а уравнение моментов составим относительно точки А. Тогда, применив уравне-1ГИЯ (4*), запишем:

i/*.. = /?-;-/?z,--Q=o, (1)

S л С/*)-- За - Р-2а + Q. а= 0.

Из уравнения (2), приняв во внимание, что Q = Р/2, найдем /?д = Р/2. Под-в уравггение (1), получим R-= Р. Итак,

2а 6)

К задаче 1.12. ставив это значение /?

Искомые давления колес автомашины на шоссе равны по модулю соответствующим реакциям и направлены противоположно, т. е. вертикально вниз.

Эту задачу можно было решить с помощью уравнений равновесия, в каждое из которых входит лишь одна неизвестная величина. Для этого вместо уравнения (1), содержащего две неизвестные величины /?д и Rq, следует составить уравне1ше моментов относительно точки В. Это уравнение удобно тем, что в него не входит /?д (момент силы относительно точки В равен нулю):

2 /Яд (/=*) = - За + Я а + Q 4а = О,

Из уравнения (4) при Q = P/2 непосредственно получим Rj = P (ср. формулу (3)).

Задача 1.13. Консольная балка AD весом Р=4 Т лежит на двух опорах В vi D, причем опора В расположена иа катках. На конце А к балке приложена вертикальная сосредоточе1Н1ая сила /-=8 Т. На участке CD на балке находится равномерно распределенная нагрузка интенсивности q = Q,o Т/м (интенсивностью называется величина силы, действующей на единицу длины). На участке АВ к балке приложена пара сил с моментом т = & Тм.

Определить опорные реакции в и Z). Размеры указаны на рисунке.

Решение. Рассмотрим равновесие консольной балки AD (участок балки АВ, расположенный вне опор, называется консолью). На балку действуют активные

К задаче 1.13.

силы: вес балки Р, приложенный в ее середине, вертикальная сила F, равнодействующая Я, распределенной нагрузки (Л = = q.CD=\ Г), приложенная в середине участка CD и направленная по вертикали вниз, и, наконец, пара сил с моментом т.

Применив закон освобождае-мости от связей, направим опорную реакцию по вертикали вверх. При равновесии балки главный вектор и главный момент равны нулю. Главный вектор равен сумме вертикальных сил F, Р, Pi, Rg и опорной реакции R (главный вектор пары сил равен нулю). Для того чтобы главный вектор был равен нулю, опорная реакция должна быть направлена вертикально.

Итак, балка находится в равновесии под действием системы параллельных сил (пару сил можно, не нарушая равновесия балки, повернуть так, чтобы силы, входящие в ее состав, были направлены вертикально), в число которых входят две неизвестные по модулю силы Рд и Pp. Следовательно, задача является статически определенной.

При решении этой задачи целесообразнее, минуя составление уравнения проекций на ось, параллельную приложет1ым силам, составить два уравнения моментов относительно точек приложе1шя и D неизвестных сил R и При этом учитываем, что сумма момешов сил, входящих в состав пары сил, вычисленная относительно любой точки, равна моменту этой пары сил. Сумму моментов сил распределенной нагрузки CD заменяем на основании теоремы Вариньона

моментом равнодействующей силы Pi. Получим:

/ИвС^лЗ-З -/и -Я-1 - Pi.3 + Ro-4 = 0, (I)

:/ о(П) = 6-m-/?-4 + p.3 + Pi.l=:0. (2)

Удобство составленных уравнений заключается в том, что в каждое из них входит только одна неизвестная величина. Из уравнений (1) и (2) находим:

/?д = -0,75 Т, /?д= 13,75 Т.

Отрицателыюе значение /?д указывает, что направление силы противоположно тому, которое изображено на рисунке, т. е. опорная реакция направлена по вертикали В1шз.

Задача 1.14. Однородная горизонтальная балка АВ весом Р=г800 и В сечении D защемлена в стене (рис. а). К балке приложены: вертикальная сосредоточен-

	1 3, - 1
		с


	* и

ная сила £=1200 и и пара сил, стремящаяся повернуть балку по

часовой стрелке. Момент пары равен /я = 600/ дж, где/ - длина свободного конца балки, рав-а) ная 2 м.

Определить реакцию и момент реактивной пары в защемленном сечении D. Размеры указаны на рисунке. Длиной защемлешюй части балки пренебречь.

Решение. Рассмотрим рав-ff) новесие балки. К ней приложены

К задаче 1.14. активные силы: Р, F я пара сил

с моментом т. Глухая заделка балки в стену препятствует перемещению балки по вертикали вниз, а также ее повороту в вертикальной плоскости под действием активных сил по часовой стрелке. Поэтому, при.менив закон освобождаемости от связей и мысленно отбросив стену, мы должны компенсировать ее действие на балку реакцией и реактивной парой сил, стремящейся повернуть балку против часовой стрелки (рис. б). Главный вектор является суммой Р, F ц реакции R (напомним, что главный вектор каждой из пар равен нулю). Так как при равновесии балки главный вектор равен нулю, а силы Р \\ F вертикальны, то реакция R также направлена вертикально (рис. б).

Повернув активную и реактивную пары так, чтобы входящие в них силы были направлены вертикально, мы получим плоскую систему параллельных сил. Данная задача является статически определенной, ибо число неизвестных равно двум (R и т^. Переходим

1 2 3 4 5 6 7 ... 51